Graphentheorie: Die Etagenbett-Vermutung ist falsch

In der Mathematik wecken bestimmte Vermutungen bei Fachleuten eine sehr starke Überzeugung – beispielsweise glauben nur wenige Mathematiker, dass die Riemann-Hypothese oder die Syrakus-Vermutung falsch sind. Manchmal erweist sich jedoch eine Aussage, die jeder für wahr hielt, als falsch. Dies geschah für die „Etagenbett-Vermutung“ in der Graphentheorie: Anfang Oktober 2024 haben Nikita Gladkov und Igor Pak von der University of California in Los Angeles sowie Aleksandr Zimin vom MIT (Massachusetts Institute of Technology), alle in den Vereinigten Staaten, haben eine Vorabveröffentlichung online gestellt, in der sie mehrere Gegenbeispiele zu einer Aussage präsentieren, die jedoch seitdem breite Akzeptanz gefunden hat seine erste Formulierung im Jahr 1985.

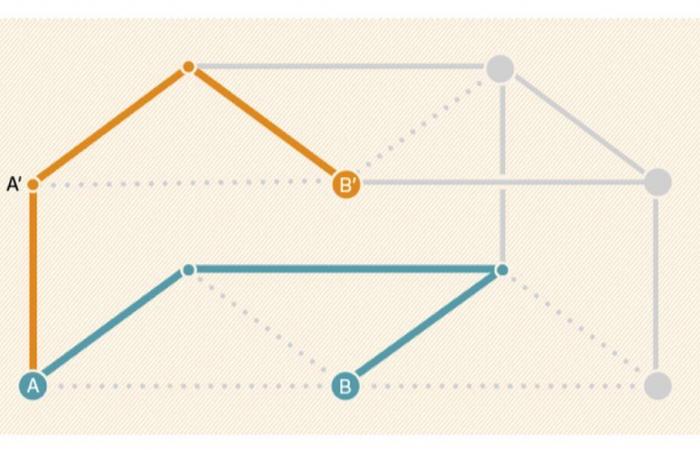
Betrachten Sie eine Grafik G verbunden (das heißt eine Reihe von Eckpunkten, die durch Kanten miteinander verbunden sind und eine einzige Struktur bilden) und duplizieren wir es, um einen zweiten Graphen zu erhalten G’identisch. Wählen wir nun eine Teilmenge der Eckpunkte von aus Gund verbinden Sie jeden von ihnen durch eine neue Kante mit dem entsprechenden Scheitelpunkt von G’. Auf diese Weise konstruieren wir einen neuen Graphen, der einem Etagenbett ähnelt, dessen unteres Bett der Graph ist Gder oben in der Grafik G’und die Beträge sind diese Kanten, die Cousin-Eckpunkte von verbinden G et G’. Stellen Sie sich nun vor, dass jede Kante dieses „Etagenbetts“ mit einer bestimmten Wahrscheinlichkeit verschwindet P. Als G verbunden war (in einem Stück), war es im ursprünglichen Diagramm immer möglich, zwei beliebige Eckpunkte von zu verbinden G – sagen wir mal A et B – durch einen kontinuierlichen Kantenpfad von G. Wie bestimmte Gipfel von G wurden mit entsprechenden Eckpunkten von verbunden G’und das G’War auch verbunden, war es auch möglich, im anfänglichen Etagenbett eine Verbindung herzustellen A an der Spitze G’entsprechend B – nennen wir es B’. Aber was passiert, wenn bestimmte Kanten zufällig entfernt werden? Die Vermutung von 1985 besagt, dass im endgültigen Etagenbett (nach probabilistischer Entfernung von Kanten) die Wahrscheinlichkeit, dass sich ein Pfad verbindet, steigt A et B ist höher als die Wahrscheinlichkeit, dass sich ein Pfad verbindet A et B’.

Bei der Arbeit an dieser Vermutung ließen sich Nikita Gladkov und seine Kollegen von den Ergebnissen von Lawrence Hollom inspirieren, einem Doktoranden an der Universität Cambridge, England, der sich ebenfalls mit dem Problem befasste, zunächst um zu zeigen, dass die Aussage richtig war. Da ihm das Ergebnis widerstrebte, konzentrierte er sich auf dieselbe Frage, übertragen auf etwas „fügsamere“ Objekte. »: Hypergraphen, eine Verallgemeinerung von Graphen, bei denen Kanten mehr als zwei Eckpunkte verbinden können. „Da ich keine großen Fortschritte machte, fing ich an, ähnliche Probleme bei Hypergraphen zu untersuchen, aber einfacher. Mir fiel jedoch auf, dass viele andere, einfachere Aussagen ebenfalls wahr sein mussten, damit die Etagenbett-Vermutung wahr war … und dass es letztendlich sehr schwierig sein würde, zu garantieren, dass diese Aussagen immer und überhaupt überprüft wurden zur gleichen Zeit! » Ergebnis: Der Forscher änderte seine Meinung und präsentierte im Juni 2024 in einer Vorveröffentlichung ein Gegenbeispiel zur Etagenbett-Vermutung für Hypergraphen.

Aus dieser Arbeit gelang es Nikita Gladkov, Igor Pak und Aleksandr Zimin wiederum, ein Gegenbeispiel zu dieser Vermutung zu konstruieren, diesmal für Graphen, für den Fall, dass die Wahrscheinlichkeit, dass Kanten verschwinden, wert ist P = 1/2. „Unser Gegenbeispiel ist ein Graph G bei 7.222 Gipfeln, sagt Nikita Gladkov. Es ist riesig, aber diese Größe kommt daher, dass wir es von Hand aus Lawrence Holloms Hypergraphen gebaut haben. Wir verstehen daher sehr gut, warum er die Vermutung nicht bestätigt! » In diesem riesigen Gegenbeispiel gibt es tatsächlich zwei Eckpunkte A et B des Diagramms G wie zum Beispiel die Wahrscheinlichkeit, dass sich ein Pfad verbindet A et B Im Etagenbett ist nach dem Löschen jeder Kante die Wahrscheinlichkeit 1/2 kleiner als die Wahrscheinlichkeit, dass sich ein Pfad verbindet A et B’. Es ist wahr, dass es lächerlich kleiner ist: Der Wahrscheinlichkeitsunterschied beträgt weniger als 10^-4331. Aber trotzdem kleiner.

Beachten Sie, dass dies immer noch der Fall ist P = 1/2 identifizierten die Forscher ein viel kleineres Gegenbeispiel: einen Graphen G auf 82 Gipfeln. Letzteres ist jedoch weniger gut verstanden: „Wir wissen nicht, wie wir ohne einen Computer auskommen sollen, um zu beweisen, dass es sich tatsächlich um ein Gegenbeispiel handelt“, beklagt Nikita Gladkov.

Igor Pak sagt gerne, dass es gut ist, von einer Woche Mathematikforschung sechs Tage den Beweisen und einen Tag den Gegenbeispielen zu widmen. Nikita Gladkov stimmt zu: „Vielleicht zeigt diese Episode, dass wir klassischen Vermutungen gegenüber skeptischer sein müssen. Wenn Sie große, nicht sehr starre Strukturen manipulieren, gibt es viele Freiheitsgrade: Dies lässt Raum für unerwartete und kontraintuitive Dinge. »